2014年08月08日
会社でのできごと
仕事をしているとたまに数学が必要になります。
とはいえ、そこまで難しい数学ではなく、考え方によっては算数程度の問題ですが、
しばらく数学、算数から離れているとなるほどと思うことがあります。
最近あった案件では、開発しているロール紙の巻き数が増えたときに、
出来上がった商品の直径がプリンタ内におさまるかというものでした。
もちろん巻き数が増え、外に行けば行くほど径の増え方は、
長さに対して減っていくため、計算をどうやって行うか悩んでいたわけですが、
何のことはない、紙の厚みと長さの面積計算で出るじゃないですか。
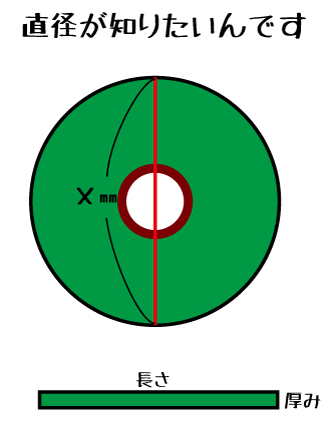
厚み×長さ=(ロールの半径)^2×3.14-(紙管の半径)^2×3.14
緑の部分がイコールになればいいわけです。
こうやって仕事上数学が顔を出すこともあり、こういう計算が楽しくてしょうがない時があります。
問題集でもやろうかなぁ~・・・。
とはいえ、そこまで難しい数学ではなく、考え方によっては算数程度の問題ですが、
しばらく数学、算数から離れているとなるほどと思うことがあります。
最近あった案件では、開発しているロール紙の巻き数が増えたときに、
出来上がった商品の直径がプリンタ内におさまるかというものでした。
もちろん巻き数が増え、外に行けば行くほど径の増え方は、
長さに対して減っていくため、計算をどうやって行うか悩んでいたわけですが、
何のことはない、紙の厚みと長さの面積計算で出るじゃないですか。

厚み×長さ=(ロールの半径)^2×3.14-(紙管の半径)^2×3.14
緑の部分がイコールになればいいわけです。
こうやって仕事上数学が顔を出すこともあり、こういう計算が楽しくてしょうがない時があります。
問題集でもやろうかなぁ~・・・。